Over the last couple of weeks, James Heathers
and I have been blogging about some rather strange articles by Dr. Nicolas Guéguen, of the Université Bretagne-Sud in
France. In this joint post, we want to
summarise the apparent issues that we have identified in this researcher’s output. Some of the points we make here have already
been touched on (or more) in an excellent article by Cathleen O’Grady at Ars Technica.
There is a lot to read
The first thing one notices in looking at his Google Scholar record is that Dr. Guéguen is a remarkably
prolific researcher. He regularly
publishes 10 or more sole-authored empirical articles per year (this total
reached 20 in 2015), many of which include extensive fieldwork and the
collection of data from large numbers (sometimes even thousands) of
participants. Yet, none of the many research assistants and other junior
collaborators who must have been involved in these projects ever seem to be
included as co-authors, or even have their names mentioned; indeed, we have yet
to see an Acknowledgments section in any sole-authored article by Dr.
Guéguen. This seems unusual,
especially given that in some cases the data collection process must have
required the investment of heroic amounts of the confederates’ time.
Much of Dr. Guéguen's research focuses on human relationships, in what
one might euphemistically term a rather "old-fashioned" way. You can get a flavour of his research
interests by browsing through his Google Scholar profile.
As well as the articles we have blogged about, he has published research on such vital topics as whether women
with
larger
breasts
get
more
invitations
to
dance
in
nightclubs (they do), whether women
are
more
likely
to
give
their
phone
number
to
a
man
if
asked
while
walking
near
a
flower
shop (they are), and whether a male bus driver is more likely to let a woman (but not a man) ride the bus for free if she touches him (we’ll let you guess the answer to this
one). One might call it “Benny
Hill
research”, although Dr. Guéguen has also
published plenty of articles on other lightweight pop-social-psychology topics
such as consumer behaviour in restaurants (does that sound familiar?) that do not immediately conjure up images of
sexual stereotypes.
Neither Dr. Guéguen’s theories, nor his experimental designs, generally
present any great intellectual challenges.
However, despite their simplicity, and the almost trivial nature of the
manipulations, his studies often produce effect sizes of the kind more normally
associated with the use of domestic
cleaning
products
against
germs. Many of the studies also seem to be run
on a production line system, with almost every combination of independent and
dependent variables being tested (something that was noted by Hans van Maanen in the Dutch newspaper De Volkskrant as far back as 2012). For example, waitresses get more tips if they
have blonde hair or use make-up or wear a red t-shirt, but women wearing red also find it easier to hitch a ride, as do women with blonde hair or larger breasts.
Those same women with blonde hair or larger breasts also get asked to dance more in
nightclubs. As well as earning her more tips if she is a waitress, using make-up also makes a woman more likely to be approached by a man in a bar, although her choice to wear make-up might
reflect the fact that she is near ovulation, at which point she is also more
likely to accept that invitation to dance; and so it goes, round and round.
It seems that some of this research is actually taken quite seriously by some psychologists. For example, it is cited
in recent work by Andrew
Elliot and colleagues at the University of
Rochester that claims to show that women wear red clothes as a sexual signal (thus also providing a piece of Dr.
Guéguen’s IV/DV combination bingo card that would otherwise have been missing). The skeptical psychologist Dr. Richard Wiseman
also seems to be something of a fan of Guéguen's work; for example, in his 2009
book 59 Seconds: Think a Little, Change a Lot, Wiseman noted that "Nicolas
Guéguen has spent his career investigating some of the more unusual aspects of
everyday life, and perhaps none is more unusual than his groundbreaking work on
breasts", and he also cited Guéguen several times in his 2013 book The As If Principle.
And of course, as is common for research with themes of sexual
attraction and other aspects of everyday human behaviour, these results readily
find their way into the popular media, such as the Daily Mail (women are more likely to give their phone number to a man who is carrying a guitar), the Guardian (people drink more in bars with louder music), The Atlantic (men think that women wearing red are more likely to be interested in sex) and the New
York Times (customers spend more money in a restaurant if it smells of lavender).
Beyond a joke
But our concerns go well beyond the apparent borderline
teenage
sexism that seems to characterise much of this
research. A far bigger scientific
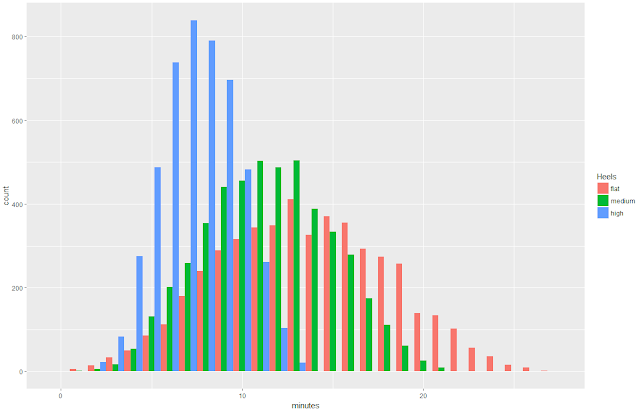
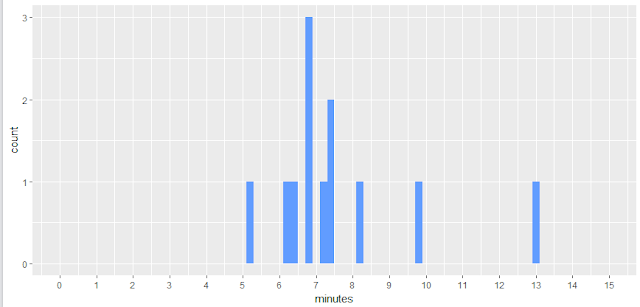
problem is the combination of extraordinary effect sizes, remarkably high (in some cases, 100%) response rates among participants recruited in the street (cf. this
study, where every single one of the 500 young female
participants who were intercepted in the street agreed to reveal their age to the
researchers, and every single one of them turned out to be aged between 18 and
25), other obvious logistical obstacles, and the large number of statistical errors or mathematically impossible
results reported in many of the analyses.
We also have some concerns about the ethicality of some of Dr. Guéguen’s field experiments. For example, in these two studies, his male confederates asked other men how likely it was that a female confederate would have sex with them on a first date, which might be a suitable topic for bar-room banter among friends but appears to us to be somewhat intrusive. In another study, women participants were secretly filmed from behind with the resulting footage being shown to male observers who rated the “sexiness” of the women’s gait (in order to test the theory that women might walk “more sexily” in front of men when they are ovulating; again, readers may not be totally surprised to learn that this is what was found). In this study, the debriefing procedure for the young female participants involved handing them a card with the principal investigator’s personal phone number; this procedure was “refined” in another study, where participants who had agreed to give their phone number to an attractive male confederate were called back, although it is not entirely clear by whom. (John Sakaluk has pointed out that there may also be issues around how these women’s telephone numbers were recorded and stored.)
It is unclear from the studies presented that any of these protocols
received individual ethical approval, as study-specific details from an IRB are
not offered. Steps to mitigate potential harms/dangers are not mentioned, even
though in several cases data collection could have been problematic, with
confederates dressing deliberately provocatively in bars and so on. Ethical
approval is mentioned only occasionally, usually accompanied by the reference
number “CRPCC-LESTIC EA 1285”. This might look like an IRB approval code of
some kind, but in fact it is just the French national science administration’s
identification code for Dr. Guéguen’s own laboratory.
It is also noteworthy that none of the articles we have read mention any
form of funding. Sometimes, however, the expenses must have been
substantial. In this study (hat tip to Harry Manley
for spotting it), 99 confederates stood outside bars and administered
breathalyser tests to 1,965 customers as they left. Even though the breathalyser device that was used is a basic model that sells for €29.95, it seems that at least 21
of them were required; plus, as the “Accessories” tab of that page shows, the
standard retail price of the sterile mouthpieces (one of which was used per
participant) before they were discontinued was €4.45 per 10, meaning that the
total cash outlay for this study would have been in the region of €1500. One would have thought that a laboratory that could
afford to pay for that out of petty cash for a single study could also pick up
the tab in a nightclub from time to time.
This has been quite the saga
It is almost exactly two years to the day since we started to put
together an extensive analysis (over 15,000 words) focused on 10 sole-authored
articles by Dr. Guéguen, which we then sent to the French Psychological Society
(SFP). The SFP’s research department agreed that we had identified a number of issues that required an answer
and asked Dr. Guéguen for his comments. Neither they nor we have received any
coherent response in the interim, even though it would take just a few minutes
to produce any of the following: (a) the names and contact details of any of
the confederates, (b) the field notes that were made during data collection,
(c) the e-mails that were presumably sent to coordinate the field work, (d)
administrative details such as insurance for the confederates and reimbursement
of expenses, (e) minutes of ethics committee meetings, etc.
At one point Dr. Guéguen claimed that he was too busy looking after a
sick relative to provide a response, circumstances which did not prevent him
from publishing a steady stream of further articles in the meantime. In the autumn of 2016, he sent the SFP a
physical file (about 500 sheets of A4 paper) containing 25 reports of field
experiments that had been conducted by his undergraduates, none of which had
any relevance to the questions that we had asked. In the summer of 2017, Dr. Guéguen
finally provided the SFP with a series of half-hearted responses to our
questions, but these systematically failed to address any of the specific
issues that we had raised. For example,
in answer to our questions about funding, Dr. Guéguen seemed to suggest that
his student confederates either pay all of their out-of-pocket expenses
themselves, or otherwise regularly improvise solutions to avoid incurring those
expenses, such as by having a friend who works at each of the nightclubs that
they visit and who can get them in for free.
We want to offer our thanks here to the officials at the SFP who spent
18 months attempting to get Dr. Guéguen to accept his responsibilities as a
scientist and respond to our requests for information. They have indicated to
us that there is nothing more that they can do in their role as intermediary,
so we have decided to bring these issues to the attention of the broader
scientific community.
Hence, this post should be regarded as a reiteration of our request for
Dr. Guéguen to provide concrete answers to the questions that we have raised.
It should be very easy to provide at least some evidence to back up his
remarkable claims, and to explain how he was able to conduct such a huge volume
of research with no apparent funding, using confederates who worked for hours
or days on end with no reward, and obtain remarkable effect sizes from
generally minor social priming or related interventions, while committing so
many statistical errors and reporting so many improbable results.
Further reading
We have made a copy of the current state of our analysis of 10 articles
by Dr. Guéguen available here, along with his replies (which are
written in French). For completeness,
that folder also includes the original version of our analysis that we sent to
the SFP in late 2015, since that is the version to which Dr. Guéguen eventually
replied. The differences between the
versions are minor, but they include the removal of one or two points where we
no longer believe that our original analysis made a particularly strong case. We also now have a better understanding of how to report some of the issues that we raise, partly because we have more experience with the application of tools such as GRIM and SPRITE.
Despite its length (around 50 pages), we hope that interested readers
will find our analysis to be a reasonably digestible introduction to the problems
with this research. Most of the original journal articles are behind paywalls, but none are
so obscure that they cannot be obtained from standard University subscriptions.
Nick Brown
James Heathers